22 November 1999: Sarah Flannery writes today the good news that she will put her paper online soon, free of any errors which may remain in this version. URL when it's available.
17 November 1999. Many thanks to Erick Wong for countless(!) typos corrected. Add William Whyte message on the successful attack on Cayley-Purser.
13 November 1999. Add transcription of Mathematica code of the RSA and C-P algorithms, which completes the HTML conversion of the full document.
12 November 1999: Add transcriptions of "The Cayley-Purser Algorithm," "Wherein lies the security of the Cayley-Purser Algorithm?," "Empirical Run-time Analysis," Post Script attack and Bibliography. Joe Author provided a PDF version of the 18 TIF images in a smaller package: http://cryptome.org/flannery-cp.pdf (603KB).
11 November 1999
Source: TIF images provided by Jean-Jacques Quisquater of 18-page hardcopy
provided by Jean-François Misarsky. Set of 18 images http://cryptome.org/flannery-cp.zip
(1.2MB)
See press release: http://europa.eu.int/comm/dg12/press/1999/pr2509en.html
See related January 1999 report: http://jya.com/flannery.htm
In equations single letters are substituted for Greek characters. Double check all equations with original images. Errata welcome; send to jy@jya.com
[Document undated; apparently September 1999. Excerpts.]
Cryptography:
An Investigation of a New Algorithm vs. the RSA
Contents
-- Mathematica Code for RSA Algorithm
-- Mathematica Code for Cayley-Purser Algorithm
Cryptography:
An Investigation of a New Algorithm vs. the RSA
As long as there are creatures endowed with language there will be the desire for confidential communication -- messages intended for a limited audience. Governments, companies and individuals have a need to send or store information in such a way that on the intended recipient is able to read it. Generals send orders, banks send fund transfers and individuals make purchases using credit cards. Cryptography is the study of methods to 'disguise' information so that only the intended receipient can obtain knowledge of its content. Public-Key Cryptography was first suggested in 1976 by Diffie and Hellman and a public-key cryptosystem is one which has the property that someone who knows only how [to] encipher ('disguise') a piece of information CANNOT use the enciphering key to find the deciphering key without a prohibitively lengthy computation. This means that the information necessary to send private or secret messages, the enciphering algorithm along with the enciphering key, can be made public-knowledge by submitting them to a public directory. The first public-key cryptosystem, the RSA Algorithm, was developed by Ronald Rivest, Adi Shamir and Leonard Adleman at MIT in 1977. This system, described below, has stood the test of time and is today recognised as a standard of encryption worldwide.
This project investigates a possible new public-key algorithm, entitled the
Cayley-Purser (CP) Algorithm and compares it to the celebrated RSA public-key
algorithm. It is hoped that the CP Algorithm is
- As secure as the RSA Algorithm and
- FASTER than the RSA Algorithm
Firstly both algorithms are presented and why they both work is illustrated. A mathematical investigation into the security of the Cayley-Purser algorithm is discussed in the main body of the report. Some differences between the RSA and the CP algorithms are then set out. Both algorithms are programmed using the mathematical package Mathematica and the results of an empirical run-time analysis are presented to illustrate the relative speed of the CP Algorithm.
RSA Public Key Cryptosystem
The RSA scheme works as follows:
Start Up: [This need be done only once.]
- Generate at random two prime numbers p and q of 100 digits or more.
- Calculate n = pq phi(n) = (p-1)(q-1) = n - (p + q) + 1.
- Generate at random a number e < phi(n) such that (e, phi(n)) = 1.
- Calculate the multiplicative inverse, d, of e (mod phi(n)) using the Euclidean algorithm.
Publish: Make public the enciphering key,
Keep Secret: Conceal the deciphering key,
Enciphering: The enciphering transformation is,
Deciphering: The deciphering transformation is,
Why the deciphering works:- The correctness of the deciphering algorithm is based on the following result due to Euler, which is a generalization of what is known as Fermat's little theorem. This result states that,
whenever (a, n) = 1, where phi(n), Euler's-phi function, is the number of positive integers less than n which are relatively prime to n.
When n = p, a prime, phi(n) = p - 1, and we have Fermat's theorem:
If p|a then ap = a = 0 (mod p), so that for any a,
Now since d is the multiplicative inverse of e, we have
Now
and
Now for P with (P, p) = 1, we have
This is trivially true when P = 0 (mod p), so that for all P, we have
Arguing similarly for q, we have for all P,
Since p and q are relatively prime, together these equations imply that for all P,
The Cayley-Purser Algorithm
Introduction
Since this algorithm uses 2 x 2 matrices and ideas due to Purser it is called the Cayley-Purser Algorithm. The matrices used are chosen from the multiplicative group G = GL(2, Zn). The modulus n = pq, where p and q are both primes of 100 digits or more, is made public along with certain other parameters which will be described presently. Since
we note that the order of G cannot be determined from a knowledge of n alone.
Plaintext message blocks are assigned numerical equivalents as in the RSA and placed four at a time in the four positions (ordered on the first index) of a 2 x 2 matrix. This message matrix is then transformed into a cipher matrix by the algorithm and the corresponding ciphertext is then extracted by reversing the assignment procedures used in the encipherment.
Because this algorithm uses nothing more than matrix multiplication (modulo n) and not modular exponentiation as required by the RSA it might be expected to encipher and decipher considerably faster than the RSA. This question was investigated, using the mathematical package Mathematica, by applying both algorithms to large bodies of text (see Tables I-IX) and it was found that the Cayley-Purser algorithm was approximately twenty-two times faster than the RSA with respect to a 200-digit modulus.
Needless to say if it could be shown that this algorithm is as secure as the RSA then it would recommend itself on speed grounds alone. The question of security of this algorithm is discussed after we have described it and explained why it works.
The CP Algorithm
Start Up: procedure to be followed by B (the receiver): [Cryptome
note: Here "in" is used for the element inclusion symbol.]
- Generate two large primes p and q.
- Calculate the modulus n = pq.
- Determine x and a in GL(2, Zn) such that xa-1 /= ax.
- Calculate b = x-1a-1x.
- Calculate g = xr ; r in N.
Publish: The modulus n and the parameters a, b, and g
Start Up Procedure to be followed by A (the sender):
In order to encipher the matrix µ corresponding to a plaintext unit
for sending to B, Person A must consult the parameters made public by B and do
the following:
- Generate a random t in N
- Calculate s = gt
- Calculate e = s-1as
- Calculate k = s-1bs
Enciphering Procedure When the above parameters are calculated, A enciphers µ via
and sends µ' and e to B
Deciphering Procedure When A receives µ' and e (s)he does the following:
Calculates
and deciphers µ' via
Why the deciphering works.
The deciphering works since
l = x-1ex= x-1(s-1as)x
= s-1(x-1ax)s : (s. being a power of x. commutes with x)
= s-1(x-1a-1x)-1s
= s-1b-1s : (recall that b = x-1a-1x)
= (s-1bs)-1
= k-1 : ( B's enciphering key )
so that
= (k-1k)µ(kk-1)
= µ.
Wherein lies the security of the Cayley-Purser Algorithm?
To find the secret matrix x, known to B alone, one might attempt to solve either the equation
or
In the first of these equations the matrix b is public and the matrix a-1 can be computed since both the matrix a and the modulus n are public.
In the second equation only the matrix g is known and it is required to solve for both the exponent r and the base matrix x. Assuming that one knew r, solving this equation would involve extracting the rth - roots of a matrix modulo the composite integer n. Even in the simplest case, where r = 2, extracting the square root of a 2 x 2 matrix modulo n requires that one be able to solve the ordinary quadratic conruence [as written]
when n = pq. It is known that the ability to solve this 'square root' problem is equivalent to being able to factor n. Thus we may regard an attack on x via the public parameter g as being computationally prohibitive.
Solving the equation
would appear the easier option for an attack on the private matrix x as it only involves solving the set of linear equations given by
However the number of possible solutions to this equation is given by the order of C(a), the centraliser of a in GL(2, Zn). By ensuring that the order of this group is extremely large one can make it computationally prohibitive to search for x.
To see why this is the case suppose that
Then
If and only if
If and only if
If and only if
Thus the number of distinct solutions of the equation is given by |C(a)| as C(a-1) = C(a).
Now C(a) will have a large order if the matrix element a has a large order.
By choosing our primes p and q to be of the form
and
where p1 and q1 are themselves prime, we can show that it is almost certainly the case that an element a chosen at random from GL(2, Zn) has a large order.
To see why, we begin by considering the homomorphism p of GL(2, Zn) onto Zn defined by sending a matrix into its determinant. The order of a matrix in GL(2, Zn) is at least that of the order of its image in Zn since ...
If r is the order of A in GL(2, Zn) and p(A) = u then Ar = I with
shows that m divides r where m is the order of u in Zn.
Thus the order of A in GL(2, Zn) is at least m. In fact
shows that Am lies in SL (2, Zn) so the matrix A will have order µ iff Am = I in SL (2, Zn).
We note also that since the maximum achievable order of an element in Zn is
| [p - 1, q - 1] | < | (p - 1)(q - 1) __________ |
= | phi(n) ___ |
| 2 | 2 |
(as (p - 1, q - 1) > 2) and since the order of SL (2, Zn) is n phi(n)(p + 1)(q + 1) the maximum achievable order of a matrix in GL(2, Zn) is
Thus if we can show that the probability of an element having a small order in Zn is negligibly small then we will have shown that the order of an element chosen at random from GL(2, Zn) is almost certainly of 'high order.'
If
and
then
with
Now the possible orders of the elements in Zn are divisors of phi(n)/2 = 2p1q1 and so are
and all of these orders are achieved by some elements. In fact by counting exactly how many elements correspond to each order we show that the probability of finding a unit in Zn of order less than p1q1 is negligibly small.
Recall that if a in Zp has order k and b in Zq has order l then the order of c in Zn where
and
is [k, l], the least common multiple of k and l.
Now the possible orders of a and b in Zp and Zq are divisors of
respectively.
The following table lists the possible orders along with the number of elements of each order.
| Z*p | Z*q | ||
| Possible Orders |
No. of elements of that order |
Possible Orders |
No. of elements of that order |
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 |
| p1 | p1 - 1 | q1 | q1 - 1 |
| 2p1 | p1 - 1 | 2q1 | q1 - 1 |
By lifting elements in pairs via the CRT we obtain the elements corresponding to the different orders in Zn along with number of elements of each order.
| Order | Number | Reason |
| 1 | 1 | [1, 1] = 1 |
| 2 | 3 | [1, 2] = [2, 1] = [2, 2] = 2 |
| p1 | p1 - 1 | [p1, 1] = p1 |
| q1 | q1 - 1 | [1, q1] = q1 |
| 2p1 | 3p1 - 3 | [2p1, 1] = [p1, 2] = [2p1, 2] = 2p1 |
| 2q1 | 3q1 - 3 | [1, 2q1] = [2, q1] = [2, 2q1] = 2q1 |
| p1q1 | p1q1 - p1 - q1 + 1 | [p1, q1] = p1q1 |
| 2p1q1 | 3p1q1 - 3p1 - 3q1 + 3 | [2p1, q1] = [p1, 2q1] = [2p1, 2q1] = 2p1q1 |
Note that if we sum all the individual counts we get exactly 4p1q1 which is the number of elements of Zn.
Explanation: To see how the number of elements corresponding to an order is obtained consider the last entry in the above array: An element of order 2p1q1 in Zn can be obtained in 3 different ways by lifting pairs of elements from Zp and Zq: One way is lifting the pair (a, b) where a has an order 2p1 and b has order q1; another by lifting the pair (a, b) where a has an order p1 and b has order 2q1 and another by lifting the pair (a, b) where a has an order 2p1 and b has order 2q1.
Regarding elements of order less than p1q1 as elements of 'low order' we obtain the probability of choosing an element of order less than p1q1 to be
| 4p1 + 4q1 - 4 ___________ |
| 4p1q1 |
This is equivalent to
In the case where p and q are both of order of magnitude 10100 this probability is approximately
which, by any standards, is negligibly small.
Some differences between the RSA and Cayley-Purser Algorithms
1. The most significant difference between the RSA and the Cayley-Purser algorithm is the fact that the Cayley-Purser algorithm uses only modular matrix multiplication to encipher plaintext messages whereas the RSA uses modular exponentiation which requires a considerably longer computation time. Even with the powerful Mathematica function PowerMod the RSA appears (see Tables I - IX) to be over 20 times slower than the Cayley-Purser Algorithm.
2. In the RSA the parameters needed to encipher -- (n, e) -- are published for the whole world to see and anyone who wishes to send a message to Bob raises their messages' numerical equivalents to the power of e modulo n. However in the Cayley-Purser algorithm the enciphering key is not made public! Only the parameters for calculating one's own key are published. This means that every sender in this system also enjoys a certain measure of secrecy with regard to their own messages. One consequence of this is that the Cayley-Purser algorithm is not susceptible to a repeated encryption attack because the sender, Alice, is the only one who knows the encryption key she used to encipher. In the RSA, however, if the order of e can be found then an eavesdropper can decipher messages.
3. Alice can choose to use a new enciphering key every time she wishes to write Bob. In the unlikely event that an eavesdropper, Eve, should find an enciphering key, she gains information about only one message and no information about the secret matrix c. By contrast, if a piece of intercepted RSA ciphertext leads to Eve being able to decipher (through repeated encryption, etc.), then she would be able to decipher all intercepted messages which are enciphered using the public exponent e.
4. In the Cayley-Purser algorithm the sender, Alice, has the ability to decipher the ciphertext which she generates using Bob's public parameters even if she loses the original message (because she knows d and therefore can get the deciphering key, k-1 = l!). Contrast this to the RSA -- Alice cannot decipher her own message once she has enciphered it using Bob's public key parameters. There is a possible advantage in this for Alice in that she could store encrypted messages on her computer ready for sending to Bob.
RSA vs. Cayley-Purser
Empirical Time-Analysis
The times taken by the Cayley-Purser and RSA algorithms (using a modulus n of the order 10200) to encipher single and multiple copies of the Desiderata (1769 characters) by Max Ehrman are given in the following tables along with the times taken by both algorithms to decipher the corresponding ciphertext.
Table I
| Running Time (Seconds) Message = 1769 characters |
||||
| Trial No. | 1 | 2 | 3 | Average |
| RSA encipher | 41.94 | 42.1 | 41.78 | 41.94 |
| RSA decipher | 40.99 | 41.009 | 41.019 | 41.009 |
| C-P encipher | 1.893 | 1.872 | 1.893 | 1.886 |
| C-P decipher | 1.502 | 1.492 | 1.492 | 1.4953 |
Table II
| Running Time (Seconds) Message = 2 * 1769 = 3538 characters |
||||
| Trial No. | 1 | 2 | 3 | Average |
| RSA encipher | 72.364 | 72.274 | 72.364 | 72.334 |
| RSA decipher | 70.942 | 70.952 | 72.144 | 71.346 |
| C-P encipher | 3.305 | 3.305 | 3.325 | 3.3016 |
| C-P decipher | 2.734 | 2.864 | 2.864 | 2.8206 |
Table III
| Running Time (Seconds) Message = 3 * 1769 = 5307 characters |
||||
| Trial No. | 1 | 2 | 3 | Average |
| RSA encipher | 103.078 | 102.808 | 103.489 | 103.125 |
| RSA decipher | 101.246 | 101.076 | 104.06 | 102.1273 |
| C-P encipher | 4.757 | 4.737 | 4.747 | 4.747 |
| C-P decipher | 3.976 | 4.086 | 4.066 | 4.0426 |
Table IV
| Running Time (Seconds) Message = 4 * 1769 = 7076 characters |
||||
| Trial No. | 1 | 2 | 3 | Average |
| RSA encipher | 134.434 | 134.323 | 134.333 | 134.363 |
| RSA decipher | 131.128 | 134.734 | 134.734 | 133.532 |
| C-P encipher | 6.159 | 6.048 | 6.109 | 6.1053 |
| C-P decipher | 5.227 | 4.967 | 4.967 | 5.05536 |
Table V
| Running Time (Seconds) Message = 12 * 1769 = 21228 characters |
||||
| RSA enc | RSA dec | C-P enc | C-P dec | |
| Time Taken | 378.078 | 371.254 | 17.435 | 14.371 |
Table VI
| Running Time (Seconds) Message = 24 * 1769 = 42456 characters |
||||
| RSA enc | RSA dec | C-P enc | C-P dec | |
| Time Taken | 509.523 | 511.455 | 22.583 | 18.767 |
Table VII
| Running Time (Seconds) Message = 48 * 1769 = 84912 characters |
||||
| RSA enc | RSA dec | C-P enc | C-P dec | |
| Time Taken | 1019.24 | 1023.95 | 44.894 | 36.823 |
Table VIII
| Running Time (Seconds) Message = 144 * 1769 = 254736 characters |
||||
| RSA enc | RSA dec | C-P enc | C-P dec | |
| Time Taken | 3154.21 | 3036.24 | 142.775 | 129.416 |
With respect to a 133MHz machine the Cayley-Purser Algorithm is on average
approximately 22 times faster than the RSA where in each case the modulus n
is of the order 10200.
Table IX
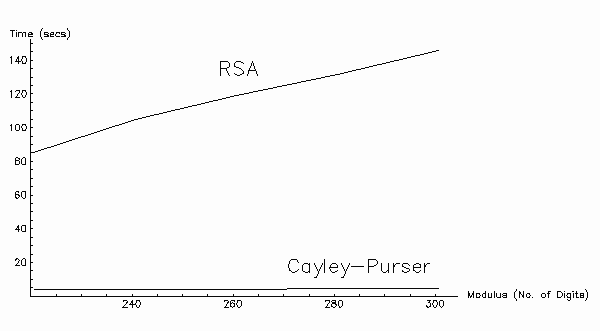
The following table illustrates the time taken for the RSA and CP Algorithms to encipher a piece of text (7076 characters in length) with varying size moduli. The ratio of the enciphering speeds is also given.
| Running Time (Seconds) Message µ containing 7076 characters |
|||
| Modulus | RSA | CP | Ratio |
| 222 digits | 84.641 | 3.916 | 21.6:1 |
| 242 digits | 104.71 | 4.036 | 25.9:1 |
| 262 digits | 118.841 | 4.276 | 27.8:1 |
| 282 digits | 131.739 | 4.326 | 30.5:1 |
| 302 digits | 145.689 | 4.487 | 32.5:1 |
Note: The difference in times taken to encipher and ecipher in the RSA depends on the binary weight of the exponents e and d.
Number of Desiderata enciphered
The piece of text used (Desiderata) contains 1769 characters.
Conclusions
This project
- (a) Shows mathematically that the CP algorithm is as secure as the RSA Algorithm.
- (b) Illustrates through an empirical run-time analysis that the CP Algorithm is FASTER to implement than the RSA Algorithm: the speed factor increasing with modulus size as shown on the following table: -
| Running Time (Seconds) Message = 4 * 1769 = 7076 characters |
|||
| Modulus | RSA | CP | Ratio |
| 222 digits | 84.641 | 3.916 | 21.6:1 |
| 242 digits | 104.71 | 4.036 | 25.9:1 |
| 262 digits | 118.841 | 4.276 | 27.8:1 |
| 282 digits | 131.739 | 4.326 | 30.5:1 |
| 302 digits | 145.689 | 4.487 | 32.5:1 |
Post Script: An Attack
on the CP Algorithm
We describe an attack on the Cayley-Purser algorithm which shows that anyone with a knowledge of the public parameters a, b and g can form a multiple x' of x. This matrix x' can then be used in conjunction with e to form l = k-1 which is the deciphering key. Thus the system as originally set out is 'broken'.
If x' = vx for some constant v and if e is known to an adversary then the calculation
yields the deciphering key k-1. Thus any multiple of x can be used to decipher.
In the CP system the matrix g is made to commute with with x so as to enable the deciphering process. This is done using the construction g = xr for some r and herein lies the weakness of the algorithm. Were g to be generated more efficiently using a linear combination of x and the identity matrix I (higher order polynomials in l reduce via the Cayley-Hamilton theorem to linear expressions in l) the system is still compromised.
If the matrix g is non-derogatory (i.e. when g is reduced mod p and mod q neither of the two matrices obtained are scalar multiples of the identity) then
( If the matrix g is derogatory then n can be factorised by calculating GCD (g11 - g22 , g12 , g21 , n) )
Now since g is non-derogatory (v, n) = 1 and
for some d in Zn.
Since
= vx-1a-1v-1x
= (v-1x)-1a-1(v-1x)
=> b = x'-1a-1x'
=> x'b = a-1x'
Substituting dI + g for x' in this last equation gives
=> db +gb = da-1 + a-1g
=> d[b - a-1] = [a-1g - gb]
Since a /= b-1 these matrices differ in at least one position. For argument's sake let a11 /= b11-1. Comparing the (1, 1) entries in the above matrix identity gives
If (a11 - b11-1)-1 exists mod n the above linear congruence is uniquely solvable for d. If not a factorisation of n is obtained.
Remark 1: This attack shows that anyone with a knowledge of the public parameters a, b and g can form a multiple x' of x. This matrix x' can then be used to form l = k-1 provided e is known. If e is transmitted securely on a once off basis then knowledge of a x' on its own is not enough to break the system, though then the Cayley-Purser Algorithm would no longer be public-key in nature.
Remark 2: The fact that a derogatory g leads to a factorisation of the modulus n was further investigated on the assumption that knowledge of n might not severely compromise the system. However in this case also a multiple of x is obtainable.
Remark 3: An analysis of the CP algorithm based on 3 x 3 matrices, though slightly more involved in its details, leads to conclusions similar to the ones just described.
Remark 4: For the sake of efficiency s should be calculated as s = ag + bI rather than as s = gt.
Mathematica Code for RSA & CP Algorithms
_______________________________________________________________
FirstPrimeAbove[n Integer]
(Clear[k];k = n;While[! PrimeQ[k],k = k + 1];k)
_______________________________________________________________
ConvertString[str_String] :=
Fold[Plus[256 #1, #2]&, 0, ToCharacterCode[str]]
_______________________________________________________________
StringToList[text_string] := Module[{blockLength =
Floor[N[Log[256, n]]], strLength = StringLength[text]},
ConvertString /@ Table[StringTake[text,{i, Min[strLength, 1 +
blockLength - 1]}],{i, 1, strLength, blockLength}]]
_______________________________________________________________
ConvertNumber[num_Integer]:=
FromCharacterCode /@ IntegerDigits[num,256]
_______________________________________________________________
ListToString[l_List] := StringJoin[ConvertNumber /@ 1]
Mathematica Code for RSA Algorithm
_______________________________________________________________
GeneratePQNED[digits_Integer] := (p = FirstPrimeAbove[
prep = Random[Integer, {10(digits-1), 10digits-1}]];
Catch[Do[preq = Random[Integer, 10^(digits-1), 10^digits-1}];
If[preq[=[re[,Throw[q = FirtPrimeAbove[preq]]], {100}]]
n = pq;e = Random[Integer, {p, n}];
While[GCD[e, (p-1) (q-1) i = 1,
e = Random[Integer, {p, n}]]; e;
d = PowerMod[e, -1 (p-1) (q-1)];)
_______________________________________________________________
RSAencNumber[num_Integer] := PowerMod[num, e, n]
_______________________________________________________________
RSAdecNumber[num_Integer] := PowerMod[num, d, n]
_______________________________________________________________
RSAenc[text_String]:=
RSAencNumber[#]& /@ StringToList[text]
_______________________________________________________________
RSAdec[cipher_List]:=ListToString[RSAdecNumber[#]&/@cipher]
Mathematica Code for Cayley Purser Algorithm
_______________________________________________________________
StringToMatrices[text_String]:= Partition[Parition[Flatten
[Append[StringToList[text],{32,32,32}]],2],2]
_______________________________________________________________
MatriceToString[l_List] :=
StringJoin [ ConvertNumber/@Flatten[1]]
_______________________________________________________________
CPpqn[digits_Integer] :=Module[{
p1 = FirstPrimeAbove[Random[Integer,
{10^(Floor[digits/2]-1), 10^(Floor[digits/2])-1}]],
q1 = FirstPrimeAbove[Random[Integer,
{10^(Floor[digits/2]-1), 10^(Floor[digits/2])-1}]],
While[PrimeQ[p = 2p1 +1], p1 = FirstPrimeAbove[p1 + 1]]; p;
While[PrimeQ[q = 2q1 +1], q1 = FirstPrimeAbove[q1 + 1]];
q; n = pq; ]
_______________________________________________________________
randmatrix := (Catch[
Do[m = Table[Random[Integer, {0, n}], {i, 1, 2}, {j, 1, 2}];
If[GCD[Mod[Det[m], n], n] == 1, Throw[m]], {1000}]])
_______________________________________________________________
inv[a_] := (d = Mod[Det[a], n]; i = PowerMod[d, -1, n];
{{Mod[i * a[[2, 2]], n], Mod[-i * a[[1, 2]], n]},
{Mod[-i * a[[2, 1]], n], Mod[i * a[[1, 1]], n]}})
_______________________________________________________________
mmul[j_, k_] := Mod[
{{Mod[j[[1, 1]]*k[[1, 1]], n] + Mod[j[[1, 2]]*k[[2, 1]], n],
Mod[j[[1, 1]]*k[[1, 2]], n] + Mod[j[[1, 2]]*k[[2, 2]], n}},
{Mod[j[[2, 1]]*k[[1, 1]], n] + Mod[j[[2, 2]]*k[[2, 1]], n],
Mod[j[[2, 1]]*k[[1, 2]], n] + Mod[j[[2, 2]]*k[[2, 2]], n]}},
n]
_______________________________________________________________
CPparameters := (identity = {{1, 0}, {0, 1}};
alpha = randmatrix; Catch[Do[chi = randmatrix;
If[mmul[chi, alpha] ! = mmul[alpha, chi],
Throw[chi]], {10000000}]]
chiinv = inv[chi]; alphainv = inv[alpha];
Catch[Do[s = Random[Integer, {2, 50}];
gamma = Mod[MatrixPower[chi, s], n];
If[gamma != identity, Throw[gamma]], {10000000}]];
Catch[Do[delta = Mod[Mod[Random[Integer, {1, n-1}]gamma, n]
+ Mod[Random[Integer, {1, n-1}]identity, n], n]
If[delta !=identity &&
mmul[delta, alpha] !=mmul[alpha, delta], Throw [delta]],
{10000000}];
beta = mmul[mmul[chiinv, aphainv], chi];
deltainv = inv[delta];
epsilon = mmul[mmul[deltainv, alpha], delta];
kappa = mmul[mmul[deltainv, beta], delta];
lambda = mmul[mmul[chiinv, epsilon], chi];)
_______________________________________________________________
CPenc[plain_String] := CPencNum [ StringToMatrices[plain]]
_______________________________________________________________
CPDecNum[l_list] := Table[mmul[mmul[lambda, l[[i]]], lambda], {i, Length[l]}]
_______________________________________________________________
CPEncNum[l_List] :=
Table[mmul[mmul[kappa, l[[i]]], kappa], {i, Length[l]}]
_______________________________________________________________
CPdec[cipher_List] := MatricesToString[CPDecNum[cipher]]
Bibliography:-
Higgins, J and Cambell, D: "Mathematical Certificates." Math. Mag 67 (1994). 21-28.
Mackiw, George: "Finite Groups of 2 x 2 Integer Matrices." Math. Mag 69 (1996). 356-361.
Meijer, A.R.: "Groups, Factoring and Cryptography." Math. Mag 69 (1996). 103-109.
Menezes, van Oorschot, Vanstone: Handbook of Applied Cryptography, CRC Press 1996.
Salomaa, Arto: Public-Key Cryptography (2 ed.). Springer Verlag 1996.
Schneier, Bruce: Applied Cryptography. Wiley 1996.
Stangl, Walter D.: "Counting Squares in n." Math. Mag 69 (1996). 285-289.
Sullivan, Donald: "Square Roots of 2 x 2 Matrices." Math. Mag 66 (1993). 314-316.
From: "William Whyte" <wwhyte@baltimore.ie> To: "Jim Gillogly" <jim@acm.org>, "John Young" <jya@pipeline.com> Subject: RE: Flannery on Cayley-Purser/RSA Date: Thu, 11 Nov 1999 18:10:21 -0000 Hi Jim, > My take from her remark in that paper is that > the system is broken as it stands, and that there's no hint yet of a > repair. This is correct; the system as published by Sarah, and posted on the Cryptome website, is broken. The reason why the project still says that it's secure is to do with the rules of the science fair that Sarah entered the project in. As you remember, she won the Young Scientist award in January with the original Cayley-Purser project, which stated that the algorithm was secure. Afterwards, myself, Michael Purser, and Sarah discovered an attack against the presented algorithm that appears pretty definitive. However, for the European Young Scientists fair, the project submitted had to be the same as the project for which you won your national prize, with the exception that you could add appendices. So that's what happened: the original project, submitted verbatim, claims the system is secure; the appendix, written afterwards, exposes the attack. It might be worth html-ising the attack and posting it, too.... Baltimore's official position is that we wish Sarah well, we continue to investigate new cryptosystems, and that the security or otherwise of the Cayley-Purser algorithm doesn't affect our core business, which is building open, standards-based Public Key Infrastructures. In a world where RSA will shortly be free, and where substantial investment has already been made in infrastructures based on existing algorithms, it seemed unlikely that Cayley-Purser would ever be a commerical proposition anyway. I did make one misleading statement, right at the start of the press excitement, when I said in various forums that the security was based on the difficulty of factorisation and was assumed to be exactly as strong as RSA. Blame the excitement of the times; we hadn't looked at the system ourselves in almost a year and in the rush I posted before pausing to make sure I had my details right. I'll do better next time (if there is a next time). Cheers, William
